anybody know what a polynomial map projection or another name for it
i cant find anything on it
cheers
Mat
anybody know what a polynomial map projection or another name for it
i cant find anything on it
cheers
Mat
You need to be a member of Land Surveyors United - Surveying Education Community to add thoughts!
Add Posts, Surveying Photos, Videos and Articles to the Surveyor Community
Add Stuff to Community
We are committed to allowing freedom of expression for all of our members, and that includes maintaining a safe space for people with opposing views to express themselves. We get posts from all over the country and even the globe, so needless to say, people come with different viewpoints on lad surveying practices and processes. We see this diversity and variety as a real strength-- dialogue and debate are an integral part of the educational process, as well as an important tool in exploring different sides of complex issues.
Replies
A map defined by one or more polynomials. Given a field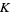 , a polynomial map is a map
, a polynomial map is a map 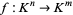 such that for all points
such that for all points 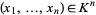 ,
,
for suitable polynomials![g_1,...,g_m in K[X_1,...,X_n]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline4.gif) . The zero set of
. The zero set of 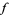 is the set of all solutions of the simultaneous equations
is the set of all solutions of the simultaneous equations 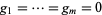 , and is an algebraic variety in
, and is an algebraic variety in 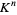 .
.
An example of polynomial map is the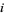 th coordinate map
th coordinate map 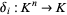 , defined by
, defined by 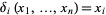 for all
for all 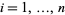 . In the language of set theory, it is the projection of the Cartesian product
. In the language of set theory, it is the projection of the Cartesian product 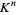 onto the
onto the 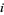 th factor.
th factor.
Polynomial maps can be defined on any nonempty subset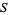 of
of 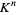 . If
. If 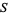 is an affine variety, then the set of all polynomial maps from
is an affine variety, then the set of all polynomial maps from 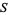 to
to 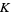 is the coordinate ring
is the coordinate ring ![K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline19.gif) of
of 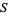 . If
. If 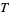 is an affine variety of
is an affine variety of 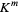 , then every polynomial map
, then every polynomial map 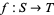 induces a ring homomorphism
induces a ring homomorphism ![F:K[T]->K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline24.gif) , defined by
, defined by 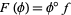 . Conversely, every ring homomorphism
. Conversely, every ring homomorphism ![G:K[T]->K[S]](http://mathworld.wolfram.com/images/equations/PolynomialMap/Inline26.gif) determines a polynomial map
determines a polynomial map 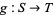 , where
, where 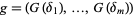 .
.
A polynomial map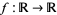 is a real-valued polynomial function. Its graph is the plane algebraic curve with Cartesian equation
is a real-valued polynomial function. Its graph is the plane algebraic curve with Cartesian equation 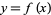 .
.
and
This looks interesting to check out and this hope this helps
Thanks Justin
But hmmmm i really dont understand what you have said
thanks for the download
cheers