DOUBLE PROPORTION MADE COMPLEX
Jerry L. Wahl
Branch of Cadastral Surveys
Bureau of Land Management
California State Office
2800 Cottage Way, E-2841
Sacramento, California 95825
ABSTRACT
Our ever increasing ability to accurately measure make it more critical that we understand the geodetic and legal concepts behind some common survey principals. As presented here, the process of determining the position of a lost section corner under the Public Land Survey rules is well known, and is even generally a matter of actual statute law. On the technical side this paper will discuss how an awareness of the unusual characteristics of the 'Public Land Survey System Datum' and the historical 'Manual' procedures lead to some interesting conclusions about the proper way to compute double proportion positions for lost corners. This discussion will include examples of how both large and small errors can creep into the process when using coordinates, especially State Plane Coordinates, and point out dangerous situations as well as proper methods to use to avoid pitfalls.
GENERAL
This presentation deals with one of those seemingly insignificant technical issues that may rise up and bite you if you are not careful. This particular discussion relates to the procedure used to restore certain lost corners in Public Land Surveys by the process called double proportion. This is a well known procedure to surveyors in such public land states who practice in suburban or rural areas. It is a process that seems straightforward on the surface, but is also sometimes misunderstood and incorrectly computed.
In defense of this technical presentation, I would like to point out that in my opinion there are many aspects to the profession of surveying. Some of the aspects on which we place the highest importance are the evaluation of evidence, discovery and analysis of prior records and application of judgement. These and other professional issues are well recognized and are significant issues in licensure. Somewhere on the list of attributes that constitute the makeup of the profession of surveying is technical expertise and knowledge of proper procedures in measurement and computation. By no means are these considerations primary, but neither are they insignificant. This discussion is almost entirely technical and one sided. Whereas in the real world I recognize that many other factors control our actions and considerations.
Before I can illustrate some of the technical quirks of double proportion, I need to briefly describe something that I refer to as 'The PLSS Datum'. This datum is simple but has some unique and even strange attributes. A thorough description of it and all it's consequences could easily be the topic of several papers, so what is outlined here is necessarily brief.
THE PLSS DATUM
The 'PLSS Datum' is the reference system by which the majority of the PLSS surveys are theoretically reported. The data being reported on a BLM or GLO Cadastral Survey plat are, of course, bearings and distances. But bearings and distances with reference to what? The current BLM Manual of Surveying Instructions, 1973 states:
"2-1. The law prescribes the chain as the unit of linear measure for the survey of the public lands. All returns of measurements in the rectangular system are made in the true horizontal distance in miles, chains and links...."
"2-17. The direction of each line of the public land surveys is determined with reference to the true meridian as defined by the axis of the earth's rotation. Bearings are stated in terms of angular measure referred to the true north or south."
"2-74. .... By basic law and the Manual requirements, the directions of all lines are stated in terms of angular measure referred to the true north (or south) at the point of record."
Distances. These and other references in the BLM and GLO Manuals make it clear that the frame of reference for distances is defined as horizontal measure in chains based on the U.S. Survey Foot at actual ground elevation. This is of importance when performing computations in projections or at sea-level when the actual lines are at a significant elevation. If you are computing proportions in a projection, the variation of elevation over a project can have a small effect, the elevation difference in essence weights the record ground measurements. This usually is a small effect unless the lines differ in elevation by a 1000 ft. or so.
Bearings: The above Manual sections and others identify the frame of reference for direction as something called 'Mean True Bearings' referenced to the true astronomic meridian '..at the point of record.' For those of you familiar with basic geodesy you will recognize that this is a basis of bearing that changes as you go east and west since the reference meridians are not parallel but converge towards the pole.
Because this is a changing reference, the direction of a straight line on the ground can be described with a forward bearing based on the meridian at the beginning end, or with a differing back bearing based on the meridian at the end point. The difference between them is the angle of convergency of the two meridians. If we want to accurately describe how far north or west the line goes in a geodetic sense, we need to use the average or 'mean' of these two values. This 'mean bearing' is essentially identical to the bearing of the traverse line with reference to it's midpoint. Thus the 'point of record' for determining the bearing of a straight traverse line can be said to be the meridian at the midpoint of the line.
Straight Lines: Therefore, one unusual byproduct of the PLSS datum is that:
Straight lines on the ground are lines of constantly changing bearing.
A straight line is basically what you would lay out by double centering or projecting a direct line of sight. The only straight line that does have a constant bearing is the meridian or north and south line. An example of a boundary that might be a straight line is one that is described as a straight line running from one physical monument to another. Such a line, if reported in the PLSS Datum would have different forward and back bearings, and different bearings at each point along it.
Rhumb Lines: It is also apparent from the various GLO and BLM Survey Manuals and the actual methods that were used to lay out the public land surveys that most boundary lines in the PLSS are intended not to be straight lines but lines of constant bearing or Rhumb Lines. Such lines cross every meridian at the same angle and are thus curved as viewed on the ground.
Therefore, another unusual byproduct of the 'PLSS datum' is that:
Lines of constant bearing are curved lines on the ground.
For example, the solar compass and transit were instruments that determined bearing at each setup, and when matched with traditional chaining, measured or laid out lines of constant bearing.
The 'Manual' discussion of latitudinal arcs illustrate one example of a rhumb line. A parallel of latitude is a line that is due East and West in the PLSS Datum. Since it crosses each meridian at a 90 degree angle, it has a mean bearing of East or West. Lines of constant bearing in the PLSS datum will appear curved on the ground. It also turns out that the mean bearing of any chord or sub-chord connecting any two points along such a line is the same as the bearing of the rhumb line itself. Thus it is possible to lay out points on a rhumb line by correcting traverse lines to their mean bearing in computations.
DOUBLE PROPORTION
Now let's look at the definition of double proportion as stated in the BLM Manual of Surveying Instructions, 1973, which states:
"5-25. The term 'double proportionate measurement' is applied to a new measurement made between four known corners, two each on intersecting meridional and latitudinal lines, for the purpose of relating the intersection to both.
In effect, by double proportionate measurement the record directions are disregarded, excepting only where there is some acceptable supplemental survey record, some physical evidence, or testimony that may be brought into the control. Corners to the north and south control any intermediate latitudinal position. Corners to the east and west control the position in longitude."
.....
"Lengths of proportioned lines are comparable only when reduced to their cardinal equivalents. "
Cardinal Equivalents: The last sentence in the above quote is one that requires some explanation. What it means is that only the easterly components (or departures) of the E-W controlling record lines are used to compute the E and W position, and only the northerly components (or latitudes) of the N-S controlling record lines are used to compute the N and S position. This is different than using the line lengths or distances on the record line.
Figure 2 illustrates the cardinal equivalents for some of the lines in the example record shown in Figure 1. Neglecting to correct the record for cardinal equivalents won't usually get you in trouble since most section lines in the original surveys are very near to cardinal and the correction is insignificant. There are, however, many situations in public land surveys where this is not the case. This situation will also occur where a retracement or subsequent GLO or BLM resurvey has reported new measurements in the PLSS datum, and the lines are distorted. The record shown in Figure 1 is a typical example, and is used to illustrate the problem.
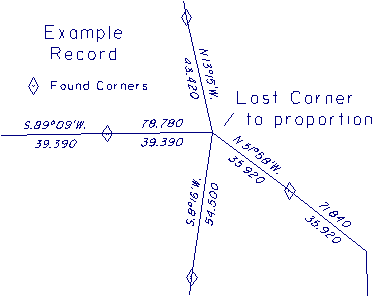
Figure 1 - Example Record
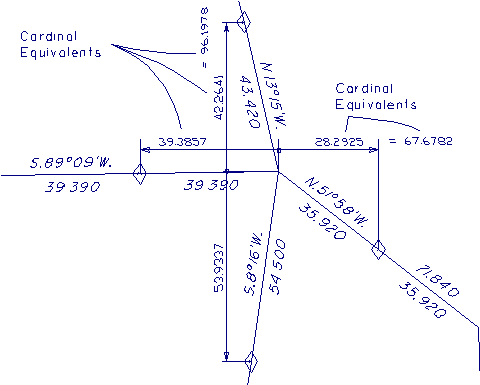
Figure 2 - Cardinal Equivalents
Cardinal offsets
The Manual of Surveying Instructions, 1973 Section 5-26 describes a process for performing a double proportion. The Manual section states:
"5-26. In order to restore a lost corner of four townships, a retracement will first be made between the nearest known corners on the meridional line, north and south of the missing corner, and upon that line a temporary stake will be placed at the proper proportionate distance; this will determine the latitude of the lost corner.
"Next, the nearest corners on the latitudinal line will be connected, and a second point will be marked for the proportionate measurement east and west; this point will determine the position of the lost corner in departure (or longitude).
"Then, through the first temporary stake run a line east or west, and through the second temporary stake a line north or south, as relative situations may determine; the intersection of these two lines will fix the position for the restored corner."
Such a process would probably be impractical in the field if followed to the letter. It is, however, a valuable way to conceptualize a proper solution of a double proportion and a good way to model a computational method.
In brief, the three part process as described consists of:
- A single proportion using the record E-W cardinal equivalents between the control E and W. In the Figure 3 example this would be point 'A'.
- A single proportion using the record N-S cardinal equivalents between the control N and S. In the Figure 3 example this would be point 'B'.
- Cardinal (true mean) offsets to intersection from those two points. In the Figure this results in point 'C'.
This last requirement can be a problem if you are not careful using coordinates, since to make the offsets cardinal requires knowledge of and proper correction to true north at those points. The common process of using the East coordinate of the E-W proportion and the North coordinate of the N-S proportion is equivalent to making a GRID offset, exagerrated In Figure 3 as point 'D', which can be incorrect.
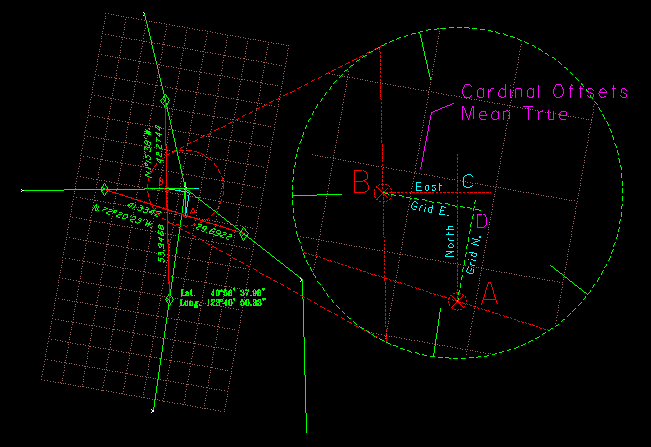
Figure 3 - Cardinal Offsets True vs Grid
Problems with State Planes.
In using state plane coordinates there are several small problems, however dealing with cardinal offsets is the most critical. This is true because with State Planes there can be a large difference between grid and true north, which is called the mapping angle. There are three methods that can be used to correct for cardinal offsets using State Plane coordinates, they are:
- Compute the mapping angle at point A to find what grid azimuth equals true North, then compute the mapping angle midway between A and B to find what grid azimuth equals mean East, them compute a grid bearing intersect. If the offsets are not large, one computation of mapping angle in the area will be adequate.
- Convert the coordinates to latitudes and longitudes at points A and B, use the latitude of B and the longitude of A and convert back to State Plane. This method essentially makes a geodetic cardinal offset.
- Convert the coordinates of the control corners to latitudes and longitudes and proportion them in a similar way to the above.
Small errors can still exist in the computation due to the datum differences. In State Planes the grid scale factor varies over the project. If you wanted to be perfect, this would require you to weight the proportions according to the mean scale factor over each line. This effect is very small. The last method is the easiest, since no correction for scale factor enters into the problem. However, performing proportions using geodetic coordinates directly can still have error if the lines are at very different elevations, since the PLSS datum represents measurements at actual average ground elevation over the line.
In the example problem, the error caused by direct proportion of the State Plane Coordiantes is in excess of 20 ft. If you used a local grid or basis of bearings the following table illustrates corresponding errors for this example.
Grid Angle Error D to C ---------------------------------- 1° 05' 20" 20.11 ft. California Zone I 0° 10' 3.40 ft. Assumed 10' off true. 0° 01' 0.65 ft. Assumed 01' off true. 0° 00' 45" 0.46 ft. Basis of Bearing, Solar 1 mile E.
SUMMARY
It can be shown that in an ideal world and with a recognition of the properties of the PLSS Datum, the only way to properly restore a corner in its true original position is by diligent application of the Manual procedures, correcting record to cardinal equivalents, proportioning and making true cardinal offsets.
Replies